Os Quatro Fundamentos dos Gráficos de Controle – Fundamento Dois
Dispersão média e desvio padrão significam a mesma coisa? O segundo Fundamento de Shewhart para os Gráficos de Controle aborda justamente esse dilema.
Fundamento Dois: Ao calcular os limites de controle (±3 sigma), você deve SEMPRE utilizar uma estatística de dispersão média
Quando se fala em dispersão média, muitas vezes associamos ao desvio padrão, certo? Ops… mas está errado! Dispersão média e desvio padrão são estatísticas diferentes!! Neste segundo fundamento, Shewhart enfatiza que os limites de controle (±3 sigma) devem ser calculados com base em uma estatística de dispersão média¹, que são estatísticas de dispersão dentro do subgrupo (gráfico Xbarra, n>1) ou entre os valores sucessivos (gráfico IX, n=1).
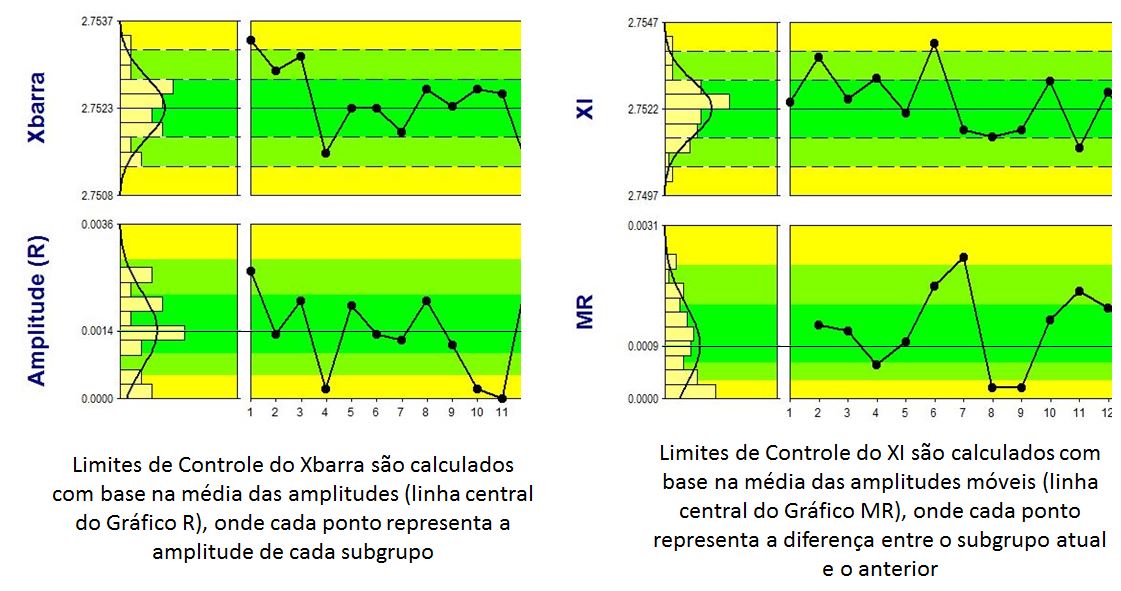
Ao utilizar uma dessas estatísticas, uma estabilidade considerável é introduzida nos cálculos dos limites. Utilizar a dispersão média dentro do subgrupo irá fornecer medidas de dispersão que são muito menos sensíveis a determinadas variações quando comparada a outras abordagens, o que diminui a probabilidade de falsos alarmes.
Ao usar uma estatística de dispersão média, aumenta-se a “robustez” do gráfico de controle. Portanto, os limites não devem ser calculados com base no desvio padrão dos indivíduos pois é mais efetivo utilizar a média das dispersões.
(1)Understanding Statistical Process Control – Donald J. Wheeler and David S. Chambers – 2010
Veja os outros fundamentos:
Fundamento Um – Utilizar limites três sigma
Fundamento Três – Definir amostragem e subgrupo racional
Fundamento Quatro – Utilizar o conhecimento adquirido

Engenheira de Alimentos pela UFSC com certificação Green Belt. Trabalha na HarboR desde 2009 atuando na capacitação, implementação e suporte técnico na área de Controle Estatístico de Processo e Qualidade em diferentes áreas da indústria.







A fundação e bem complexa,para colocar em prática no dia a dia.