En este post hablaremos acerca del Diagrama de Caja (Box Plot) y cómo él puede ayudarte aún más en la interpretación de los datos. Ya discutimos en posts anteriores otras herramientas de la calidad para análisis de datos, como la Gráfica de Control, Gráfica de Dispersión, Gráfica de Pareto e Histograma (disponibles sólo en portugués). Sin embargo, cuando deseamos comparar productos, máquinas, turnos o lotes, la herramienta complementaria para este tipo de análisis es el Diagrama de Caja.

El Diagrama de Caja es una gráfica utilizada para auxiliar en la identificación de valores atípicos de un conjunto de datos (llamados outliers), así como comparar la dispersión entre dos o más conjunto de datos (análisis de simetría). También es muy útil para analizar la dispersión de los conjuntos de datos alrededor de los límites de especificación y del valor objetivo.

 

Comprendiendo el Diagrama de Caja

Cuando analizamos un conjunto de datos es usual utilizar un Histograma para entender la tendencia central y la distribución de los datos. Sin embargo, cuando deseamos comparar más de un conjunto de datos utilizamos el Diagrama de Caja. Como vemos en la imagen abajo, el Histograma es la vista frontal de la distribución de los datos, mientras que el Diagrama de Caja es la vista superior de un histograma.

 

 

El Diagrama de Caja se basa en la localización de los cuartiles (cuartil₁, cuartil₂ o mediana, cuartil₃), que son tres valores que dividen un conjunto de datos (ordenado de manera creciente) en cuatro sub-intervalos, cada uno con el 25% de las observaciones.

 

 

¿Cuál es el significado de estos intervalos?

• 1° intervalo cuartílico: está delimitado por el Valor Mín Q1 (cuartil₁). A partir del punto más pequeño del conjunto de datos hasta el segmento vertical, se encuentra el 5% de los valores del conjunto de datos; del segmento vertical hasta el primer segmento del cuadro amarillo, se encuentra el 20% de los valores del conjunto de datos; totalizando el 25% de los valores. Este intervalo es el primer “bigote” del Diagrama de Caja.
• 2° intervalo cuartílico: está delimitado por el Q1 y Q2 (cuartil₂ – mediana). En este intervalo se encuentra el 25% de los valores del conjunto de datos y está representado por la primera parte de la caja amarilla.
• 3° intervalo cuartílico: está delimitado por el Q2 y Q3 (cuartil₃). En este intervalo se encuentra el 25% de los valores del conjunto de datos y está representado por la segunda parte de la caja amarilla.
• 4° intervalo cuartílico: está delimitado por el Q3 y Valor Máx. A partir del final de la caja amarilla hasta el segmento vertical, se encuentra el 20% de los valores del conjunto de datos; del segmento vertical al punto más grande del conjunto de datos, se encuentra el 5% restante de los valores del conjunto de datos, totalizando los últimos 25% de los valores. Este intervalo está representado por el segundo “bigote” del Diagrama de Caja.

 

Ejemplo Práctico

En este ejemplo vamos a comparar la dispersión de los datos entre dos productos (Partes) distintos. “Eje Rueda Delantera” y “Eje Rueda Trasera”. La dispersión es representada por el rango (máximo – mínimo) de los datos, cuanto mayor sea el rango es decir que los datos poseen mayor variación.

 

 

Con el Diagrama de Caja, imagen arriba, conseguimos responder fácilmente a las siguientes preguntas:

• ¿Cuál es el producto que presenta la menor variación? Eje Rueda Trasera

Este producto puede ser el ejemplo para conocer las causas asignables del proceso para obtener menor variación del producto.

• ¿Cuál es el producto que presenta la mayor variación? Eje Rueda Delantera

Como es el producto con la mayor dispersión de los datos, debemos realizar un análisis más profundo, enfocado y ágil de este proceso con el objetivo de disminuir la variación en el producto.

 

Pero, ¿dónde ocurre esta variación?

Para enriquecer nuestro análisis, vamos a utilizar el mismo Diagrama de Caja añadiendo más un nivel de estratificación, las características (pruebas) que fueran evaluadas en cada pieza. Tres puntos diferentes (A, B y C) de diámetros externos (DE) se evalúan para definir si la pieza está conforme al estándar, respetando sus límites de especificación.

 

 

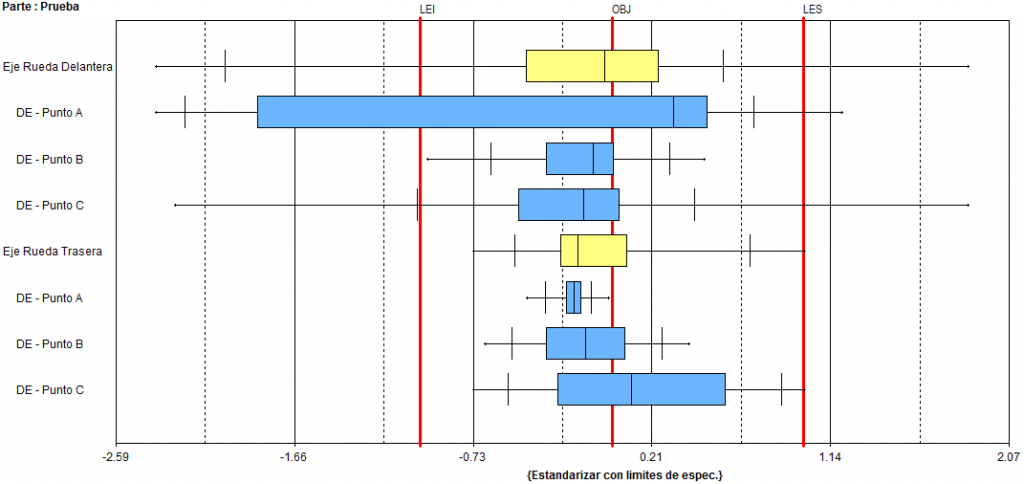
En esta visualización del Diagrama de Caja, conseguimos ver la distribución de los datos relacionados con las características evaluadas alrededor de los límites de especificación¹. De inmediato, el Diagrama de Caja ya nos responde a las siguientes preguntas:

• ¿Cuál es la característica que presenta la mayor variación? Eje Rueda Delantera – DE – Punto A

Más del 25% de los datos se producen fuera del límite de especificación inferior (LEI), se debe investigar  más a fondo el proceso para conocer las causas de esta variación.

• ¿Cuál es la única característica dentro de los límites de especificación para el Eje de la Rueda Delantera? DE – Punto B

Su distribución está completamente dentro de los límites de especificación. En este caso los esfuerzos pueden ser dirigidos en el intento de centralizar la mediana del proceso junto al objetivo de la especificación.

• ¿Cuál característica tiene el bigote más grande? Eje Rueda Delantera – DE – Punto C

Bigotes muy grandes son una señal de que los valores mínimo e máximo deben ser investigados. Estos puntos atípicos se llaman outliers, y pueden revelar errores de medición o de ejecución de procedimiento. Si los datos se refieren a errores de medición es necesario corregirlos para que no interfieran en la toma de decisiones. De lo contrario, estos puntos pueden contener información relevante acerca de tu proceso, siendo necesario identificar la causa de esta variación para que no vuelva a ocurrir.

• ¿Cuál es la característica que presenta la menor variación? Eje Rueda Trasera – DE – Punto A

Esta es la característica donde se encuentra la menor variación de todo el estudio, esto también debe ser tenido en cuenta para entender el éxito de este proceso e intentar aplicar las mismas condiciones en los otros procesos.

 

El Diagrama de Caja es una excelente herramienta de análisis que ayuda en la interpretación y comparación de datos de diferentes procesos, productos, características, lotes y otros. Él nos proporciona información acerca de la ubicación, dispersión y outliers de tu conjunto de datos.

Con el Software InfinityQS tu puedes fácilmente construir un Diagrama de Caja para el análisis de tus datos. Si tu empresa ya utiliza InfinityQS y deseas conocer más información de esta gráfica en InfinityQS, haga cli aquí (disponible sólo en portugués) y acceda a nuestro documento de soporte.

(1) Cada característica tiene un límite de especificación diferente, para que sea posible evaluar los límites en una misma gráfica los datos fueran estandarizados alrededor del objetivo especificado.