O que considerar no momento de definir estratégias de amostragens? Qual a melhor maneira de organizar os dados em subgrupos? Parecem perguntas simples, porém é fundamental conhecer e entender suas respostas para que as análises gráficas de fato sejam válidas. É sobre isso que vamos tratar neste post, que é o tema apresentado no Terceiro Fundamento de Shewhart para os Gráficos de Controle.

 

Fundamento Três: Amostragem e Subgrupo Racional

Amostragem Racional

Amostras racionais são tomadas levando em consideração a forma como o processo é medido e o quê, onde e quando é medido. Seguem algumas perguntas para ajudar a definir uma amostragem racional:

• Quem coletará os dados?

Avalie as habilidades do operador para coletar dados. Quanto tempo o operador dispõe? O operador tem recursos adequados para coletar os dados?

• O que será medido?

Foque em características chave. Sempre lembre que medir custa dinheiro! Devemos focar nas características que são críticas para controlar o processo.

• Onde a amostra será retirada?

A amostra deve ser tomada em um ponto do processo que permita que os dados sejam usados para o controle do processo.

• Quando a amostra será retirada do processo?

As amostras devem ser tomadas com frequência suficiente para refletir as mudanças do processo.

• Porque estamos medindo?

As informações coletadas precisam possibilitar a tomada de ações no processo. Os dados serão usados para controle do processo ou controle do produto?

• Como os dados serão coletados?

Deve ser estabelecido um procedimento padrão para a coleta de dados. Instrumentos e operadores diferentes não devem interferir nos resultados obtidos.

• Quantos itens serão medidos?

As amostras devem ser aleatórias e representativas. O tamanho da amostra deve ser suficiente para o controle do processo, sem ser grande demais, causando grandes custos, perdas de tempo ou produtividade.

Subgrupo Racional

Uma vez que as amostragens foram realizadas de forma racional, os dados obtidos também devem ser agrupados de forma racional. Este agrupamento é chamado de subgrupo, ou seja, é um conjunto de indivíduos registrados como um ponto no gráfico. Subgrupo racional é aquele onde há baixa probabilidade de apresentar variações por causas atribuíveis dentro do subgrupo. Existem alguns princípios para agrupar subgrupos que devem ser usados na construção de Gráficos de Controle, são eles:

• Nunca agrupe coisas diferentes em um subgrupo:

Não misture informações de processos diferentes, produtos diferentes, momentos diferentes… Informações de fontes distintas precisam ser avaliadas individualmente, do contrário, informações importantes podem ser mascaradas e conclusões errôneas podem ser tomadas.

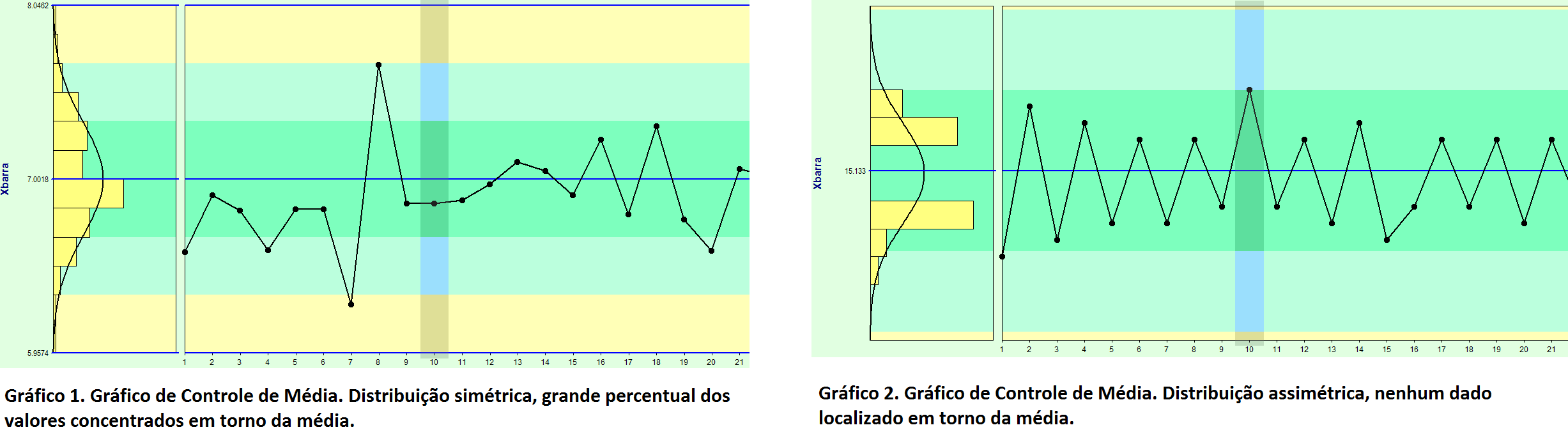
Por exemplo, produtos de diferentes linhas de produção não devem ser misturados em um subgrupo. No Gráfico 1, podemos ver que a distribuição é simétrica, não indica a mistura de informações diferentes. Já no Gráfico 2, vemos que a distribuição dos dados se acumula afastada da média do processo, indicando uma mistura de informação (por exemplo, a saída de duas linhas diferentes). Neste caso, os dados devem ser analisados separadamente, para que as informações transpareçam a realidade da produção.

• Minimize a variação em cada subgrupo

A variação dentro de cada subgrupo interfere diretamente nos limites de controle. Quando você minimiza a variação dentro do subgrupo você estará criando um Gráfico de Controle que será sensível aos sinais do processo (causas atribuíveis – grandes variações), pois somente os ruídos (causas aleatórias – pequenas variações) serão considerados para definir a variação do processo.

Se somente variações aleatórias existirem nos subgrupos, quaisquer diferenças entre ou dentro dos subgrupos serão atribuídas a causas atribuíveis.

• Maximize a oportunidade de variação entre os subgrupos

Se existe a possibilidade de interferências, certifique-se de que elas estejam em subgrupos diferentes. O gráfico de média analisa as diferenças entre os subgrupos. Ele usa a variação dentro do subgrupo para saber quanta variação deve ser ignorada entre os subgrupos e assim detectar as causas atribuíveis atuando.

• Faça média de coisas similares, não de coisas diferentes

O objetivo de utilizar a média de subgrupos é agrupar coisas onde somente ruídos (variações inerentes ao processo) atuam para que seja fácil identificar quando um sinal está atuando no processo.

• Utilize o gráfico adequado para o tipo de dado

Se valores individuais são coletados, então utilize subgrupos de tamanho um, que serão plotados em um gráfico XI. No caso de múltiplas coletas em um mesmo momento, utilize a média para definir o subgrupo e plotar os dados em um gráfico XBarra.

• Estabeleça procedimento padrão de amostragem

Tamanho e frequência de amostras devem ser mantidas. Assim como técnicas de coleta de dados não devem variar de acordo com o instrumento e operador que realiza as medições.

Portanto, quando você toma cuidado em como amostrar e agrupar os seus dados, você ganha o poder de transformar seu Gráfico de Controle em uma ferramenta informativa, eficaz e confiável para a tomada de decisão.

 

Veja os outros fundamentos:

Fundamento Um – Utilizar limites três sigma

Fundamento Dois – Utilizar estatística da dispersão média

Fundamento Quatro – Utilizar o conhecimento adquirido